Bem-vindo ao Suporte da Microsoft
Entre para que possamos atender melhor Entrar
Olá, , bem-vindo ao Suporte da Microsoft.
Tópicos mais populares
conta e armazenamento da Microsoft
Windows e dispositivos

Encontrar Copilot Pro
O mais novo membro da família Copilot oferece acesso prioritário aos principais modelos de IA e, para assinantes do Microsoft 365 Home e Microsoft 365 Family, um companheiro de IA nos aplicativos do Microsoft 365 que você já usa todos os dias.
Explorar
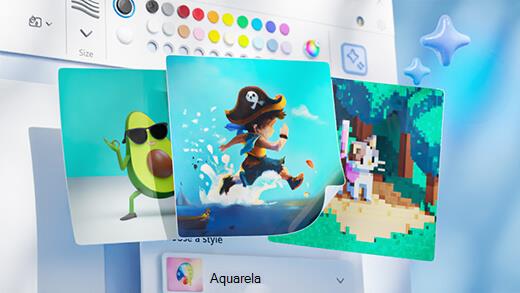
Gerar arte com o Cocriador do Paint
Crie uma arte incrível com apenas algumas palavras. O Cocriador do Microsoft Paint ajudará você a liberar sua criatividade e fazer suas próprias obras de arte com a ajuda da IA.

Obter mais com a IA no Windows
O Windows é a primeira plataforma de computador a fornecer assistência centralizada de IA. Saiba como obter e criar mais com o Copilot no Windows.

O Office agora é Microsoft 365
A página inicial das suas ferramentas e conteúdo favoritos. Agora, com novas maneiras de ajudá-lo a encontrar, criar e compartilhar seu conteúdo, tudo em um só lugar.

Centro de Treinamento do Microsoft 365
Seja produtivo rapidamente com esses vídeos, tutoriais e recursos do Microsoft 365
História de sucesso de uma pequena empresa
Descubra como o proprietário de uma pequena empresa, Dave Quick, reconstruiu sua empresa e recuperou sua vida cotidiana com o Microsoft 365.

Mais opções de suporte
Fale com o suporte
Suporte corporativo
Segurança e privacidade
Mais suporte

Faça mais rápido com o Microsoft 365
Crie e compartilhe rapidamente um conteúdo que se destaca, gerencie sua agenda com facilidade, conecte-se facilmente com outras pessoas e aproveite a tranquilidade - tudo isso com o Microsoft 365.
