Willkommen beim Microsoft-Support
Bitte melden Sie sich an, damit wir Ihnen besser helfen können. Anmelden
Hallo, , willkommen bei Microsoft-Support.
Beliebte Themen
Microsoft 365
Microsoft-Konto und -Speicher

Entdecken Sie Microsoft Copilot
Erreichen Sie alles, was Sie sich vorstellen können, mit Ihrem KI-Begleiter in den Apps, die Sie bereits täglich verwenden.
Erkunden
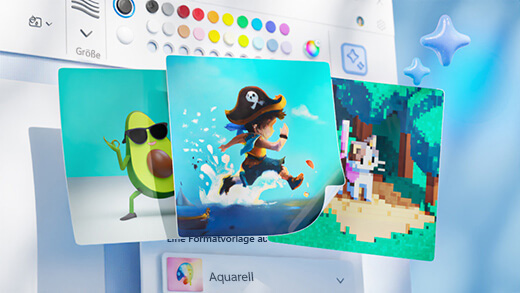
Generieren von Grafiken mit Paint Cocreator
Erschaffen Sie mit nur wenigen Wörtern beeindruckende Kunstwerke. Microsoft Paint Cocreator hilft Ihnen, Ihre Kreativität zu entfesseln und Ihre eigenen Kunstwerke mit Hilfe von KI zu erschaffen.

Erreichen Sie mehr mit KI in Windows
Windows ist die erste PC-Plattform, die zentralisierte KI-Unterstützung bietet. Erfahren Sie, wie Sie mit Copilot in Windows mehr erreichen und erstellen.

Office ist jetzt Microsoft 365
Die Startseite für Ihre bevorzugten Tools und Inhalte. Jetzt mit neuen Möglichkeiten, Ihre Inhalte zu suchen, zu erstellen und zu teilen – alles an einem zentralen Ort.

Microsoft 365-Schulungscenter
Mit diesen Microsoft 365 Videos, Tutorials und Ressourcen werden Sie schnell produktiv.
Erfolgsgeschichten von Microsoft 365 für kleine Unternehmen





Wenn Sie ein Besitzer eines kleinen Unternehmens sind
Finden Sie die Informationen, die Sie benötigen, um Ihr kleines Unternehmen mit Microsoft 365 aufzubauen, zu führen und zu erweitern.
Mehr Supportoptionen
Kontaktieren Sie den Support.
Enterprise Support
Datenschutz & Sicherheit
Mehr Unterstützung

Mehr mit Copilot Pro
Steigern Sie Ihre Kreativität und Produktivität mit einer erstklassigen Copilot-Erfahrung. Laden Sie die Copilot-App für eine einmonatige kostenlose Testversion von Copilot Pro herunter.

